Лингвофорум

Цитата: Волод от июля 25, 2024, 06:40Але коли в першому наближенні то тому, що сума усіх коренів рівняння має дорівнювати якомусь коефіцієнту у рівнянні.

Теорема Виета жи есть.

https://ru.wikipedia.org/wiki/Формулы_Виета

Цитата: maratique от июля 24, 2024, 21:33А вы можете мне ответить на вопрос: почему между иррациональными корнями любого уравнения обязательно есть хоть какая-нибудь симметрия? На математических форумах меня посылают изучать теорию Галуа, но хотелось бы простого объяснения. Филосовского.

Мабуть, питання для мене занадто фундаментальне.
Але коли в першому наближенні то тому, що сума усіх коренів рівняння має дорівнювати якомусь коефіцієнту у рівнянні.
Тобто корені рівняння аналогічні шматочкам пазла, вони мають мати форму що дозволить скласти з них картину. Тобто ці шматочки мають стикуватися один з одним.

История простая:

линейные и квадратные уравнения умели решать уже в глубокой древности

3000 лет застоя

кубическое уравнение решили примерно одновременно с открытием Америки Колумбом

уравнение четвёртой степени решили в той же итальянской тусовке через примерно 40 лет

уравнение пятой степени не могли решить после этого 300 лет. Лагранж написал труд про перестановки корней, т. е. про симметрию.

С помощью его идей Руффини и Абель доказали, что уравнения пятой степени не решаются.

Галуа использовал эти идеи для уравнений не только пятой, но любой степени.

А вы можете мне ответить на вопрос: почему между иррациональными корнями любого уравнения обязательно есть хоть какая-нибудь симметрия? На математических форумах меня посылают изучать теорию Галуа, но хотелось бы простого объяснения. Филосовского.

В английской Википедии написано, что достоверно не известно как Сципионе дель Ферро открыл формулу решения кубического уравнения. Но предполагается, что он использовал тот факт, что является корнем квадратного уравнения , и предположил, что решает кубическое уравнение .

А так да, это очень трудно было. Ни греческие гении, ни исламские не смогли до этого допереть. Удивительно, конечно. Фигня, если подумать.

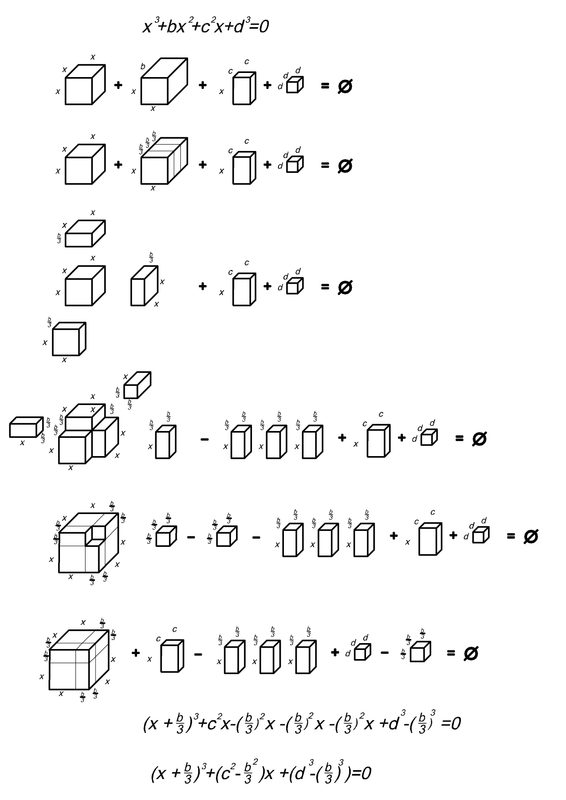
Чому ніхто не звернув увагу на помилку в самому першому рівнянні?

Цитата: Karakurt от июня 29, 2024, 11:18Любое полное уравнение 3 степени приводится к неполному, устраняя х^2? ИИ сказал что это невозможно.

А Википедия сказала, что это делается подстановкой x=y−b/3a.

ІІ=ШІ

Як буде час і творче натхнення, то намалюю збирання кубика, що з'їдає квадрат ікса.
Я не малював його, бо це було мені не цікаво.
А що ІІ каже про перетворення повного квадратного рівняння в неповне?