- Добро пожаловать на Лингвофорум.
Автор Bhudh
- января 16, 2011, 19:08Цитата: hurufuКакой ужасный внетем пошел...
Ну какой же это ↓ внетем?‥
Цитата: Квас
Автор Квас
- января 16, 2011, 18:47Цитата: Драгана от января 16, 2011, 18:35
А что такое бутылка Клейна?
Такая двумерная поверхность. Вырезаем квадрат и склеиваем противоположные стороны в направлениях, указанных стрелками:

Получается двумерная поверхность. Её можно вложить в четырёхмерное пространство, а в трёхмерное — не получается, только с самопересечениями. Получается как-то так:


Автор Драгана
- января 16, 2011, 18:35Цитата: Квас от января 16, 2011, 16:03А что такое бутылка Клейна?
Мне кажется, иногда четвёртое измерение удобно было бы цветом изображать. Тогда было бы ясно, что бутылка Клейна без самопересечений.
Автор Квас
- января 16, 2011, 18:19Цитата: hurufu от января 16, 2011, 18:16
IMHO, мне кажется, что легче представлять четырехмерные объекты таки прохождением через наше пространство, нежели проекцией.
Сферу хорошо проецировать. Посмотрел — круг. С другой стороны — тоже круг. Сверху — опять круг. Верти — не верти...
Автор hurufu
- января 16, 2011, 18:16IMHO, мне кажется, что легче представлять четырехмерные объекты таки прохождением через наше пространство, нежели проекцией.
Хотя конечно еще более понятнее алгебраическое описание .
.
Какой ужасный внетем пошел...
Хотя конечно еще более понятнее алгебраическое описание
 .
.Какой ужасный внетем пошел...
Автор Квас
- января 16, 2011, 18:14В любом случае, мне кажется, что интуитивное представление о сфере (и окружности) основано на постоянстве кривизны. А у них в википедии постоянством кривизны не пахнет.
Автор Квас
- января 16, 2011, 18:12Цитата: Bhudh от января 16, 2011, 18:00
(wiki/ru) Гиперсфера
Какая-то там бредовая картинка. По ней можно увидеть, что сфера — многообразие? (То есть небольшие окрестности точек трёхмерной сферы топологически устроены абсолютно так же, как открытые трёхмерные шары.)
Автор arseniiv
- января 16, 2011, 18:06Цитата: Квас от января 16, 2011, 17:20Ой. Я имел ввиду первое, так что правильно поняли.
Тьфу, я подумал на ограниченные. А почему из незамкнутых-то нельзя?
Автор Bhudh
- января 16, 2011, 18:00Автор Марбол
- января 16, 2011, 17:33Здравствуйте!
Оченьзнакомо. А многомерная сфера в декартовых координатах как омжет быть построена?
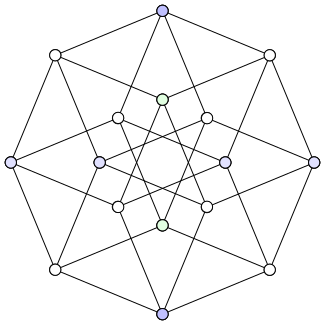
Цитата: Bhudh от января 14, 2011, 00:11
Это, кстати, можно и по-другому показать.
Вот, к примеру, тессеракт:
А вот интересная его стереопара:
Оченьзнакомо. А многомерная сфера в декартовых координатах как омжет быть построена?